具有矢量分析和问题示例的运动学材料

章节和矢量分析

运动学

运动学 是讨论物体运动的运动科学，无论作用在物体上如何 (物体的质量被忽略). 因此，只要运动才能通过速度V和 /或加速度确定，就由物体传播的距离.

常规的直运动 (GLB)

常规的直运动 (GLB) 是在水平方向上的直运动，固定的V速度 (加速度a = 0), 因此，S所传递的距离仅由一定时间内的固定速度决定.
Untuk mendapatkan rumus GLB didasari oleh aturan Hukum Newton I ( s f = 0 ).

s = x = v . t ;
a = dv/dt = dv/dt = 0
V = DS/DT = DS/DT = TETAP

标志d (不同之处) 陈述平均值.
标志d (微分) 陈述瞬时价值.

GLBB

不规则的直运动变化 (GLBB) 是沿水平方向的直运动，速度V可以随着固定的加速而随时变化. 对物体从初始静音或从初始速度开始的对象的另一种理解将发生变化，因为存在加速度 (a = +) 或放缓 (a = -).
通常GLBB基于牛顿二世定律 ( S F = M . 一个 ).

VT = V0 + 在
VT2 = V02 + 2 作为
S = V0 T + 1/2 T2

VT =对象的瞬时速度
V0 =对象的初始速度
S =距离旅行的距离
f(t) =时间t的功能t

V = DS/DT = F (t)a = dv/dt = tetap

术语 : 如果两个物体移动并且两个相遇，则两个对象要走的距离是相同的.

自由秋季运动

y = h = 1/2 GT2

t =Ö(2 H/g)

yt = g t =Ö(2 G H)
是从H的一定高度沿垂直方向落下的物体而没有初始速度的运动 (v0 = 0), 因此，物体的运动仅是由地球g的重力引起的.
g =地球重力的加速.
y = h =沿垂直方向的物体传播的路径,(从第一件事的位置衡量).
t =对象需要路径所需的时间.

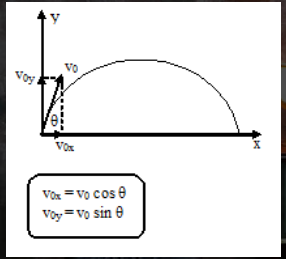
Gerak Vertikal Keatas

是在垂直方向上以V0的初始速度抛出的物体的运动, 最高a = -g (朝着重力方向).
因此物体必须达到最大高度 (H麦克斯): VT = 0
在向上解决垂直运动问题时, 通过假设地面位置为y =，可以更容易完成 0.

单位矢量.

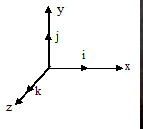
1.导致X轴单元i的向量.
2.Vektor yang mengarah sumbu y satuannya j.
3.导致Z轴单元k的向量.

位置向量

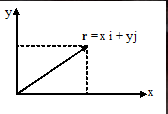
r是位置向量, X指定X和Y轴上的坐标点是轴上的坐标点.

位移矢量

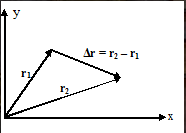
位移是在特定时间间隔内变化的粒子位置.

和 ΔR解释了转移向量，R1和R2解释了第一个和第二位置向量.

平均速度向量

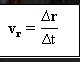
是传输矢量的结果 (Δr) 与时间间隔 (Δt).

VR =平均速度矢量.

速度向量片刻

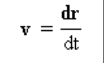
是位置函数的第一个导数 (r) 反对时间 (t).

平均加速度向量

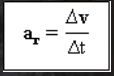
是速度的变化 (Δv) 时间间隔 (Δt) 肯定.

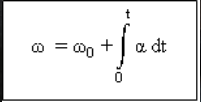
瞬时加速矢量

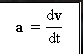
是速度函数的第一个衍生物 (v) 反对时间 (t).

确定速度向量的位置向量.

确定加速矢量的速度向量.

循环运动

1. 常规的循环运动 (GMB)
GMB是具有角速度的圆形运动 (w) 保持。线性速度V的方向将始终冒犯轨道, 意义 ,等于切向速度的方向，而V的速度始终固定 (因为w仍然存在). 使径向AR加速度仍然很大，但方向变化. AR也可以称为centripetal/selbrifugal加速度始终 | v.

v = 2pr/t = w rar = v2/r = w2 rs = q r
2. 循环运动不规则地变化 (GMBB)
GMBB是一种圆形运动，具有固定的角加速度.
在此运动中，有一个切向加速度在=线性加速度, 是一个加速度，其方向通向圆路径 (随速度V的方向拉伸).
a = dw/dt =马 / r
at = dv/dt = a r
t =周期 (第二)
r =圆手指.
A =角加速度/角度 (行/det2)
AT =切向加速 (m/det2)
W =角速度/角度 (行/IT)
Q =大角度 (弧度)
S =弧的长度
线性数量的线性之间的关系:
VT = V0 + t wt
S = V0 T + 1/2 到T2UD W0 + 在
q = W0 + 1/2 T2
角位置 (θ) 和角转移 (Δθ).

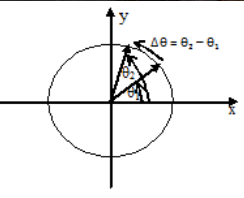
和 Δθ 可以解释角传递, θ1 和 θ2 解释第一和第二角的位置.

平均角速度

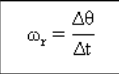
是角传递的结果 (Δθ) 与时间间隔 (Δt).

Kecepatan sudut sesaat

是角度位置函数的第一个导数 (θ) 反对时间 (t).

平均角加速度向量

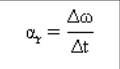
是角速度的变化 (Δω) 时间间隔 (Δt) 肯定.

向量角度加速一会儿

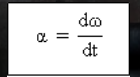
是角速度函数的第一个衍生物 (ω) 反对时间 (t).

确定角速度的角度位置.

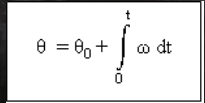
确定角加速度的角速度.

抛物线运动

达到最大高度的时间.

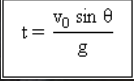
最大高度

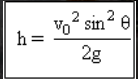
最大覆盖范围/水平距离.

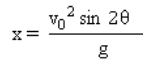
问题的示例 :

1. 如果pertikel以位置方程式r = 5t2移动 + 1, T1 =之间的平均速度 2 S和T2 = 3 s…
一个. 25 多发性硬化症
b. 30 多发性硬化症
c. 35 多发性硬化症
d. 40 多发性硬化症
e. 45 多发性硬化症

信息:
一个. 首先计算R1 → T1 = 2 s
R1 = 5T2 + 1 = 5 (2)2 + 1 = 5 . 4 + 1
R1 = 21 m
b. 计算R2 → T2 = 3 s
R1 = 5T2 + 1 = 5 (3)2 + 1 = 5 . 9 + 1
R1 = 46 m
c. 计算位移 Δr.
ΔR = R2-R1 = 46 -21 = 25 m.
d. 计算VR的平均速度.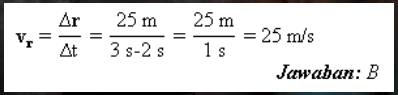
2. 在平面中移动的点对象的位置由方程式表示: r = (5 T2 – 2 t) 我 + 6 T J带有米为米和t的规定，. 对象在时间t =时的加速度值 2 Sekon是…
一个. 6 M/S2
b. 10 M/S2
c. 18 M/S2
d. 24 M/S2
e. 28 M/S2