Bab siri geometri dan contoh masalah siri geometri

Definisi Siri Geometri

Definisi urutan Geometri adalah urutan di mana setiap suku diperoleh dari produk suku sebelumnya dengan pemalar. Siri geometri adalah urutan yang memenuhi hasil bagi istilah dengan istilah berturut-turut yang mempunyai nilai tetap.

Contohnya :
turutan geometri ialah a,b, dan c kemudian c / b = b / a = pemalar. Hasil bagi istilah yang berdekatan disebut nisbah (r).

Contohnya terdapat siri geometri seperti di bawah

U1, U2, U3 ,… ,A 1, A
Kemudian U2 / U1, U3 / U2,…, Un / Un-1 = r
Bagaimana menentukan suku ke-n dari barisan geometri?
Lihat penjelasan di bawah

U3/U2 = r jadi, U3 = U2.r = a.r.r = ar2
Un / Un-1 = r jadi, Satu = Satu-1. r = arn-2.r = arn-2 + 1 = arn-1
Maka dapat disimpulkan bahawa formula geometri bagi garis geometri istilah ke-9 adalah Un = arn-1

a= nisbah kadar awal r.

Formula Siri Geometri

Nombor pertama dari urutan geometri dipanggil urutan geometri. Andai suku ke-n dari barisan geometri dirumuskan an = a1rn – 1, maka siri geometri boleh ditulis sebagai,

Sn = a1 + a1r + a1r2 + a1r3 … + a1r-1

Sekiranya kita mengalikan siri dengan –r kemudian menambahkannya mengikut siri asal, maka ia akan mendapat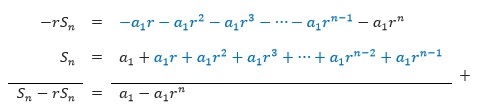

Hingga mendapat Sn – rSn = a1 – a1rn. Dengan menyelesaikan persamaan untuk Sn, kemudian dapatkan

Hasil di atas adalah formula bagi jumlah sebutan n pertama bagi urutan geometri yang tidak terhingga.

Jumlah n Suku Pertama Barisan Geometri

Diberikan barisan geometri dengan suku pertama a1 dan rasio r, bilangan sebutan n pertama iaitu

boleh dikatakan: Jumlah garis geometri sama dengan perbezaan istilah pertama dan istilah n + 1, kemudian dibahagi dengan 1 tolak nisbah.

Contoh Soalan Siri Geometri

Soalan: Kira jumlahnya 9 suku pertama pada barisan an = 3n.

Jawapan:

jumlah 9 istilah pertama dapat dilambangkan dalam notasi sigma di bawah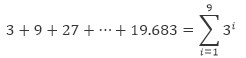

Dari siri yang diperoleh istilah pertama a1 = 3, rasio r = 3, dan bilangan sebutan n = 9. Dengan menggunakan formula untuk bilangan sebutan pertama n

Kemudian, jumlah sembilan suku pertama dari barisan an = 3n itu dia 29.523.

Demikianlah pembahasa mengenai deret geometri, Semoga bermanfaat

Artikel lain :

• Virus : Struktur, Pengelasan, Bentuk, Sejarah dan Definisi dan Contoh Virus
• Medan magnet : Perwatakan, Pemahaman dan Rumusan

 

The post Formula Siri Geometri dan Contoh Soalan Seri Geometri muncul pertama kali di halaman ini.