Bab Kinematika dan analisis vektor

Kinematik adalah sains gerakan yang membincangkan pergerakan objek tanpa mengira daya yang bertindak pada objek (jisim objek diabaikan). Jadi jarak yang dilalui oleh objek semasa pergerakannya hanya dapat ditentukan oleh halaju v dan / atau pecutan a.

Gerakan Lurus Biasa (GLB)

Gerakan Lurus Biasa (GLB) adalah gerakan lurus dalam arah mendatar dengan halaju malar v (pecutan a = 0), supaya jarak yang dilalui oleh S hanya ditentukan oleh kelajuan tetap untuk masa tertentu.
Untuk mendapatkan formula GLB berdasarkan peraturan Newton's Law I ( S F = 0 ).

s = X = v . t ;
a = Dv / Dt = dv / dt = 0
v = DS / Dt = ds / dt = tetap

Tanda D (beza) menyatakan nilai purata.
Tanda d (pembezaan) mewakili nilai seketika.

GLBB

Perubahan Gerak Lurus dengan Susunan (GLBB) adalah gerakan lurus dalam arah mendatar dengan halaju v yang boleh berubah pada bila-bila masa kerana pecutan berterusan. Pengertian lain adalah bahawa objek yang menggunakan kekuatan gerakan dari keadaan awalnya yang beristirahat atau dimulai dengan halaju awal akan mengubah kecepatannya akibat pecutan. (a = +) atau perlambatan (a = -).
biasanya GLBB berdasarkan Undang-undang Newton II ( S F = m . a ).

vt = v0 + a.t
vt2 = v02 + 2 sebuah S
S = v0 t + 1/2 a t2

vt = halaju sekejap objek
v0 = halaju awal objek
S = jarak yang ditempuh benda
f(t) = fungsi masa t

v = ds / dt = f (t)a = dv / dt = tetap

Syarat : Sekiranya dua objek bergerak dan saling bertemu, jarak yang akan dilalui kedua-dua objek adalah sama.

Gerakan jatuh percuma

y = h = 1/2 gt2

t = Ö(2 h / g)

yt = g t = Ö(2 g h)
adalah pergerakan objek jatuh pada arah menegak dari ketinggian tertentu h tanpa halaju awal (v0 = 0), sehingga menjadikan gerak benda hanya disebabkan oleh gravitasi bumi g.
g = pecutan kerana graviti.
y = h = lintasan-lintasan yang ditempuh oleh benda pada arah vertikal,(diukur dari posisi benda mula-mula).
t = masa yang diperlukan untuk objek itu bergerak.

Gerak Vertikal Keatas

adalah gerakan objek yang dilemparkan dengan halaju awal v0 dalam arah menegak, sehingga a = -g (melawan arah graviti).
jadi objek harus mencapai ketinggian maksimumnya (h maks): Vt = 0
Di dalam penyelesaian soal gerak vertikal keatas, lebih senang diselesaikan dengan menganggap kedudukan di atas tanah adalah untuk Y = 0.

Vektor unit.

 

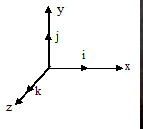
1.Vektor yang menunjukkan unit x paksi i.
2.Vektor yang menunjukkan paksi-y ialah j.
3.Vektor yang menunjukkan paksi-z ialah k.

Vektor kedudukan

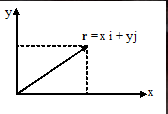
Dengan r ialah vektor posisi, x menyatakan titik koordinat pada sumbu x dan y ialah titik koordinat pada sumbu y.

Vektor perpindahan

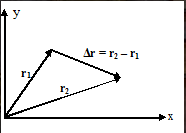
Perpindahan adalah perubahan kedudukan zarah dalam masa tertentu.

Dengan Δr menerangkan vektor anjakan dan r1 dan r2 menerangkan vektor kedudukan pertama dan kedua.

Vektor halaju purata

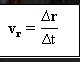
adalah hasil bagi vektor anjakan (Δr) dengan selang waktu (Δt).

Di mana vr = vektor halaju purata.

Vektor halaju sekejap

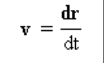
adalah terbitan pertama fungsi kedudukan (r) terhadap masa (t).

Vektor pecutan purata

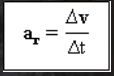
mewakili perubahan rentak (Δv) dalam selang masa (Δt) pasti.

Vektor pecutan seketika

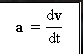
adalah terbitan pertama fungsi kelajuan (v) terhadap masa (t).

Tentukan vektor kedudukan vektor halaju.

Tentukan vektor halaju dari vektor pecutan.

Gerakan Bulat

• 1. PERGERAKAN PEKELILING PESANAN (GMB)
  GMB adalah gerakan bulat pada halaju sudut (w) Arah halaju linier v akan selalu menyinggung lintasan, tujuan itu ,sama dengan arah halaju tangen sementara halaju v sentiasa malar (kerana w tetap). menjadikan pecutan radial adalah magnitud tetap tetapi berubah arah. ar juga boleh dipanggil pecutan sentripetal / sentrifugal berterusan | v.

  v = 2pR / T = w Rar = v2 / R = w2 Rs = q R

• 2. CIRCLE MOVES CHANGE REGULAR (GMBB)
  GMBB adalah gerakan bulat dengan pecutan sudut tetap a.
  Dalam gerakan ini terdapat pecutan tangen aT = pecutan linear, ialah pecutan ke arah lintasan bulat (berhimpit dengan arah kecepatan v).
  a = Dw / Dt = aT / R
  aT = dv / dt = a R
  T = perioda (kedua)
  R = jejari bulatan.
  a = pecutan sudut / sudut (rad / det2)
  aT = pecutan tangen (m / det2)
  w = kecepatan angular/sudut (rad / det)
  q = besar sudut (radian)
  S = panjang lengkok
  Hubungan antara kuantiti linear dan kuantiti sudut:
  vt = v0 + a t wt
  S = v0 t + 1/2 a t2Þ w0 + a t
  Þ q = w0 + 1/2 a t2
• Kedudukan sudut (θ) dan perpindahan sudut (Δθ).
• 

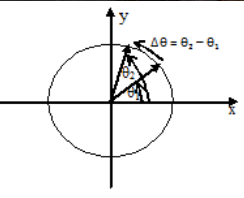
Dengan Δθ dapat menjelaskan anjakan sudut, θ1 dan θ2 menerangkan kedudukan sudut pertama dan kedua.

Halaju sudut purata

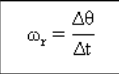
merupakan hasil bagi antara perpindahan sudut (Δθ) dengan selang waktu (Δt).

Halaju sudut sekejap

adalah terbitan pertama fungsi kedudukan sudut (θ) terhadap masa (t).

Vektor pecutan sudut min

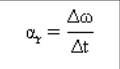
mewakili perubahan dalam halaju sudut (Δω) dalam selang masa (Δt) pasti.

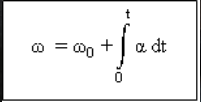
Vektor pecutan sudut seketika

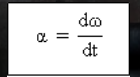
adalah turunan pertama fungsi halaju sudut (ω) terhadap masa (t).

Menentukan kedudukan sudut dari halaju sudut.

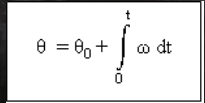
Tentukan halaju sudut dari pecutan sudut.

Gerakan Parabola

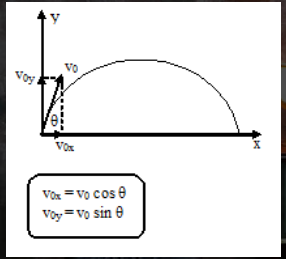
Masa untuk mencapai ketinggian maksimum.

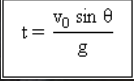
Ketinggian maksimum

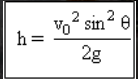
Jangkauan maksimum / jarak mendatar.

 

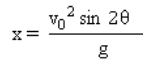
Contoh Soal :

1. Jika sebuah pertikel bergerak dengan persamaan posisi r = 5t2 + 1, halaju purata antara t1 = 2 s dan t2 = 3 s adalah…
A. 25 Cik
B. 30 Cik
C. 35 Cik
D. 40 Cik
E. 45 Cik

• Maklumat:
  a. Pertama, hitung r1 → t1 = 2 s
  r1 = 5t2 + 1 = 5 (2)2 + 1 = 5 . 4 + 1
  r1 = 21 m
  b. Hitungkan r2 → t2 = 3 s
  r1 = 5t2 + 1 = 5 (3)2 + 1 = 5 . 9 + 1
  r1 = 46 m
  c. Mengira anjakan Δr.
  Δr = r2-r1 = 46 -21 = 25 m.
  d. Mengira halaju purata vr.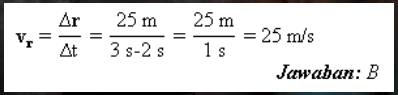
• 
• 2. Kedudukan sebuah benda titik yang bergerak dalam bidang datar dinyatakan dengan persamaan: r = (5 t2 – 2 t) i + 6 t j dengan sebutan r dalam meter dan t dalam beberapa saat. Nilai pecutan objek pada t = 2 kedua adalah…
  A. 6 m / s2
  B. 10 m / s2
  C. 18 m / s2
  D. 24 m / s2
  E. 28 m / s2
• 

3. Halaju sudut objek dikenali sebagai berikut:
ω = (3t2 + 6t – 2) rad / s, t dalam beberapa saat.
Pada t = 0,5 kedua, nilai pecutan sudut objek adalah…
A. 15 rad / s2
B. 12 rad / s2
C. 9 rad / s2
D. 6 rad / s2
E. 3 rad / s2

4. Objek dalam gerakan lurus mempunyai persamaan untuk halaju:
v = (3 – 6t) i + (4 + 8t) j
Pergerakan objek semasa selang dari detik kedua hingga detik ketiga adalah…
A. 10 m
B. 14 m
C. 25 m
D. 42 m
E. 60 m

5. Peluru ditembak dengan kecepatan awal 100 m / s dan sudut ketinggian 30o. Sekiranya graviti berada di mana ia berada 10 m / s2, maka diperlukan peluru untuk mencapai titik tertinggi adalah…
A. 2 kedua
B. 5 kedua
C. 6 kedua
D. 10 kedua
E. 15 kedua

 

Demikianlah pembahasan mengenai

The post Bahan Kinematik dengan Analisis Vektor dan Masalah Contoh muncul pertama di halaman ini.