Bab Kinematika dan analisis vektor

Kinematika merupakan Ilmu gerak yang membahas gerak suatu benda tanpa memandang gaya yang bekerja pada benda tersebut (massa benda diabaikan). Jadi jarak yang ditempuh oleh benda selama geraknya hanya bisa ditentukan oleh kecepatan v dan atau percepatan a.

Gerak Lurus Beraturan (GLB)

Gerak Lurus Beraturan (GLB) merupakan gerak lurus pada arah mendatar dengan kecepatan v tetap (percepatan a = 0), sehingga nya jarak yang ditempuh S hanya ditentukan oleh kecepatan yang tetap dalam waktu tertentu.
Untuk mendapatkan rumus GLB didasari oleh aturan Hukum Newton I ( S F = 0 ).

s = X = v . t ;
a = Dv/Dt = dv/dt = 0
v = DS/Dt = ds/dt = tetap

Tanda D (selisih) menyatakan nilai rata-rata.
Tanda d (diferensial) menyatakan nilai sesaat.

GLBB

Gerak Lurus Berubah Beraturan (GLBB) merupakan gerak lurus pada arah mendatar dengan kecepatan v yang dapat berubah setiap saat karena adanya percepatan yang tetap. pengertian yang lain benda yang sedang melakukan gaya gerak dari keadaan awal nya diam atau mulai dengan kecepatan awal akan terjadi perubahan pada kecepatannya dikarenakan ada percepatan (a= +) atau perlambatan (a= -).
biasa nya GLBB didasari oleh Hukum Newton II ( S F = m . a ).

vt = v0 + a.t
vt2 = v02 + 2 a S
S = v0 t + 1/2 a t2

vt = kecepatan sesaat benda
v0 = kecepatan awal benda
S = jarak yang ditempuh benda
f(t) = fungsi dari waktu t

v= ds/dt = f (t)a = dv/dt =tetap

Syarat : Jika dua benda bergerak dan kedunya saling bertemu maka jarak yang akan ditempuh kedua benda adalah sama.

Gerak jatuh bebas

y = h = 1/2 gt2

t = Ö(2 h/g)

yt = g t = Ö(2 g h)
adalah gerak jatuh benda pada arah vertikal dari ketinggian h tertentu tanpa kecepatan awal (v0 = 0), sehingga menjadikan gerak benda hanya disebabkan oleh gravitasi bumi g.
g = percepatan gravitasi bumi.
y = h = lintasan-lintasan yang ditempuh oleh benda pada arah vertikal,(diukur dari posisi benda mula-mula).
t = waktu yang diperlukan oleh benda untuk menempuh lintasannya.

Gerak Vertikal Keatas

merupakan gerak benda yang dilempar dengan suatu kecepatan awal v0 pada arah vertikal, sehingga a = -g (melawan arah gravitasi).
jadi suatu benda harus mencapai ketinggian maksimum (h maks): Vt = 0
Di dalam penyelesaian soal gerak vertikal keatas, lebih mudah diselesaikan dengan menganggap posisi di tanah adalah untuk Y = 0.

Vektor satuan.

 

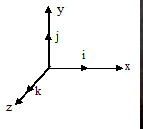
1.Vektor yang mengarah sumbu x satuannya i.
2.Vektor yang mengarah sumbu y satuannya j.
3.Vektor yang mengarah sumbu z satuannya k.

Vektor posisi

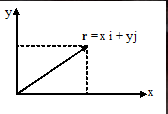
Dengan r ialah vektor posisi, x menyatakan titik koordinat pada sumbu x dan y ialah titik koordinat pada sumbu y.

Vektor perpindahan

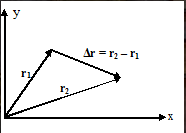
Perpindahan merupakan perubahan posisi suatu partikel dalam selang waktu tertentu.

Dengan Δr menjelaskan vektor perpindahan dan r1 dan r2 menjelaskan vektor posisi pertama dan kedua.

Vektor kecepatan rata-rata

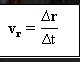
merupakan hasil bagi antara vektor perpindahan (Δr) dengan selang waktu (Δt).

Dengan vr = vektor kecepatan rata-rata.

Vektor kecepatan sesaat

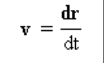
merupakan turunan pertama dari fungsi posisi (r) terhadap waktu (t).

Vektor percepatan rata-rata

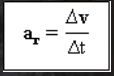
merupakan perubahan kecepatan (Δv) dalam selang waktu (Δt) tertentu.

Vektor percepatan sesaat

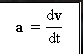
merupakan turunan yang pertama dari fungsi kecepatan (v) terhadap waktu (t).

Menentukan vektor posisi dari vektor kecepatan.

Menentukan vektor kecepatan dari vektor percepatan.

Gerak Melingkar

• 1. GERAK MELINGKAR BERATURAN (GMB)
  GMB merupakan gerak melingkar dengan kecepatan sudut (w) tetap.Arah dari kecepatan linier v akan selalu menyinggung lintasan, maksudnya ,sama dengan arah kecepatan tangensial sedangkan besar kecepatan v selalu tetap (karena w tetap). menjadikan adanya percepatan radial ar yang besarnya tetap akan tetapi arahnya berubah-ubah. ar bisa disebut juga percepatan sentripetal/sentrifugal yang selalu | v.

  v = 2pR/T = w Rar = v2/R = w2 Rs = q R

• 2. GERAK MELINGKAR BERUBAH BERATURAN (GMBB)
  GMBB merupakan gerak melingkar dengan percepatan sudut a tetap.
  Dalam gerak ini terdapat percepatan tangensial aT = percepatan linier, merupakan percepatan yang arahnya mengarah pada lintasan lingkaran (berhimpit dengan arah kecepatan v).
  a = Dw/Dt = aT / R
  aT = dv/dt = a R
  T = perioda (detik)
  R = jarijari lingkaran.
  a = percepatan angular/sudut (rad/det2)
  aT = percepatan tangensial (m/det2)
  w = kecepatan angular/sudut (rad/det)
  q = besar sudut (radian)
  S = panjang busur
  Hubungan besaran linier dengan besaran angular:
  vt = v0 + a t wt
  S = v0 t + 1/2 a t2Þ w0 + a t
  Þ q = w0 + 1/2 a t2
• Posisi sudut (θ) dan perpindahan sudut (Δθ).
• 

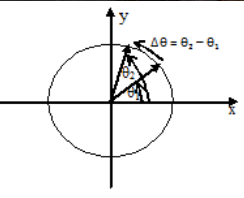
Dengan Δθ dapat menjelaskan perpindahan sudut, θ1 dan θ2 menjelaskan posisi sudut pertama dan kedua.

Kecepatan sudut rata-rata

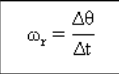
merupakan hasil bagi antara perpindahan sudut (Δθ) dengan selang waktu (Δt).

Kecepatan sudut sesaat

merupakan turunan pertama dari fungsi posisi sudut (θ) terhadap waktu (t).

Vektor percepatan sudut rata-rata

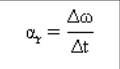
merupakan perubahan kecepatan sudut (Δω) dalam selang waktu (Δt) tertentu.

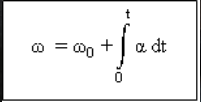
Vektor percepatan sudut sesaat

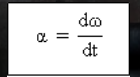
adalah turunan yang pertama dari fungsi kecepatan sudut (ω) terhadap waktu (t).

Menentukan posisi sudut dari kecepatan sudut.

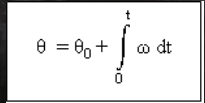
Menentukan kecepatan sudut dari percepatan sudut.

Gerak Parabola

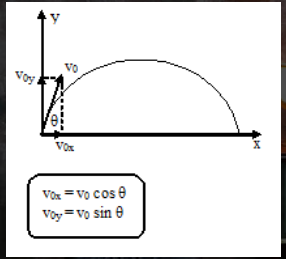
Waktu untuk mencapai pada ketinggian maksimum.

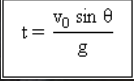
Ketinggian maksimum

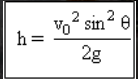
Jangkauan maksimum/jarak mendatar.

 

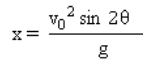
Contoh Soal :

1. Jika sebuah pertikel bergerak dengan persamaan posisi r = 5t2 + 1, kecepatan rata-rata antara t1 = 2 s dan t2 = 3 s adalah…
A. 25 m/s
B. 30 m/s
C. 35 m/s
D. 40 m/s
E. 45 m/s

• Keterangan:
  a. Terlebih dahulu hitung r1 → t1 = 2 s
  r1 = 5t2 + 1 = 5 (2)2 + 1 = 5 . 4 + 1
  r1 = 21 m
  b. Menghitung r2 → t2 = 3 s
  r1 = 5t2 + 1 = 5 (3)2 + 1 = 5 . 9 + 1
  r1 = 46 m
  c. Menghitung perpindahan Δr.
  Δr= r2-r1 =46 -21 =  25 m.
  d. Menghitung kecepatan rata-rata vr.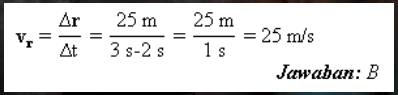
• 
• 2. Kedudukan sebuah benda titik yang bergerak dalam bidang datar dinyatakan dengan persamaan: r = (5 t2 – 2 t) i + 6 t j dengan ketentuan r dalam meter dan t dalam sekon. Nilai percepatan benda pada saat t = 2 sekon adalah…
  A. 6 m/s2
  B. 10 m/s2
  C. 18 m/s2
  D. 24 m/s2
  E. 28 m/s2
• 

3. Kelajuan anguler suatu benda diketahui sebagai berikut:
ω = (3t2 + 6t – 2) rad/s, t dalam sekon.
Pada t = 0,5 sekon, nilai percepatan sudut benda itu adalah…
A. 15 rad/s2
B. 12 rad/s2
C. 9 rad/s2
D. 6 rad/s2
E. 3 rad/s2

4. Benda yang bergerak lurus memiliki persamaan kecepatan:
v = (3 – 6t) i + (4 + 8t) j
Perpindahan benda tersebut selama selang waktu sekon kedua sampai sekon ketiga adalah…
A. 10 m
B. 14 m
C. 25 m
D. 42 m
E. 60 m

5. Sebuah peluru ditembakkan dengan kecepatan awal 100 m/s dan sudut elevasi 30o. Jika gravitasi ditempat itu 10 m/s2, maka waktu yang diperlukan peluru tersebut untuk mencapai titik tertinggi adalah…
A. 2 sekon
B. 5 sekon
C. 6 sekon
D. 10 sekon
E. 15 sekon

 

Demikianlah pembahasan mengenai

The post Materi Kinematika Dengan Analisis Vektor Beserta Contoh Soal appeared first on this page.