Capitolo sulle serie geometriche ed esempi di domande sulle serie geometriche

Comprendere le serie geometriche

La definizione di sequenza geometrica è una sequenza in cui ogni termine è ottenuto moltiplicando il termine precedente per una costante. Una serie geometrica è una sequenza che soddisfa il quoziente di un termine con il termine consecutivo precedente avente valore costante.

Per esempio :
La sequenza geometrica è a,B, e c quindi c/b = b/a = costante. Il quoziente dei termini adiacenti si chiama rapporto (R).

Ad esempio, una serie geometrica si trova come di seguito

U1, U2, U3 ,… ,E-1, E
Quindi U2/U1, U3/U2,…, Uno/Uno-1 = r
Come determinare l'ennesimo termine di una successione geometrica?
Leggi la spiegazione qui sotto

U3/U2 = r jadi, U3 = U2.r = a.r.r = ar2
Un/Un-1 = r jadi, Uno = Uno-1. r = arn-2.r = arn-2+1 = arn-1
Si può quindi concludere che la formula per l'n-esimo termine della serie geometrica è Un = arn-1

UN= rapporto r del termine iniziale.

Formula della serie geometrica

La somma dei primi n termini di una successione geometrica si chiama serie geometrica. Se l'n-esimo termine di una successione geometrica è formulato come an = a1rn – 1, allora la serie geometrica può essere scritta come,

Sn = a1 + a1r + a1r2 + a1r3 … + a1r-1

Se moltiplichiamo la serie per –r quindi lo aggiunge alla serie originale, allora otterrai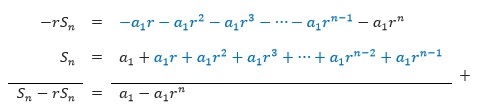

Finché non lo ottieni Sn – rSn = a1 – a1rn. Risolvendo l'equazione per Sn, allora prendi

Il risultato sopra è la formula per la somma dei primi n termini di una sequenza geometrica infinita.

Somma di n primi termini di una successione geometrica

Data una successione geometrica con primo termine a1 e rapporto r, la somma dei primi n termini cioè

si può dire: La somma di una successione geometrica è uguale alla differenza tra il primo termine e l'ennesimo termine + 1, poi dividi per 1 meno il rapporto.

Esempi di domande sulle serie geometriche

Domanda: Calcola l'importo 9 primo termine della riga an = 3n.

Risposta:

Quantità 9 Il primo termine può essere indicato nella notazione sigma di seguito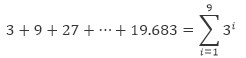

Da questa serie si ottiene il primo termine a1= 3, rasio r = 3, e il numero di termini n = 9. Utilizzando la formula per la somma dei primi n termini

Per, la somma dei primi nove quarti della riga an = 3n questo è 29.523.

Tale è chi parla delle serie geometriche, Spero che sia utile

Altri articoli :

• Virus : Struttura, Classificazione, Modulo, Storia, definizione ed esempi di virus
• Campo magnetico : Natura, Definizione e formula

 

Il post Formule delle serie geometriche ed esempi di domande sulle serie geometriche è apparso per primo in questa pagina.