Chapter Kinematics and vector analysis

Kinematics is the Science of motion that discusses the motion of an object regardless of the force acting on the object (mass of objects is ignored). So the distance traveled by an object during its motion can only be determined by velocity v and or acceleration a.

Irregular Straight Motion (GLB)

Irregular Straight Motion (GLB) is a straight motion in the horizontal direction with a fixed speed v (acceleration a = 0), so the distance traveled by S is only determined by a fixed speed within a certain time.
To get the GLB formula based on Newton's Law I rules ( S F = 0 ).

s = X = v . t ;
a = Dv/Dt = dv/dt = 0
v = DS/Dt = ds/dt = tetap

Mark D (difference) stated average value.
Signs d (differential) declare a momentary value.

GLBB

Irregular Motion Changes Irregularly (GLBB) is a straight motion in the horizontal direction with velocity v that can change at any time due to a constant acceleration. Another understanding is that the object that is doing the force of motion from its initial state is stationary or starts with the initial velocity, there will be a change in its speed due to acceleration (a= +) or slowing down (a= -).
GLBB is usually based on Newton's Law II ( S F = m . a ).

vt = v0 + a.t
vt2 = v02 + 2 a S
S = v0 t + 1/2 a t2

vt = the instantaneous velocity of objects
v0 = the initial velocity of the object
S = distance traveled
f(t) = function of time t

v= ds/dt = f (t)a = dv/dt =tetap

Terms : If two objects move and they meet, the distance to be traveled by the two objects is the same.

Free fall motion

y = h = 1/2 gt2

t = Ö(2 h/g)

yt = g t = Ö(2 g h)
is the motion of falling objects in the vertical direction from a certain height h without the initial velocity (v0 = 0), thus making motion only due to the gravity of the earth g.
g = earth's gravitational acceleration.
y = h = the trajectories traveled by the object in the vertical direction,(measured from the position of the first object).
t = the time required for the object to travel through its path.

Vertical Movement Above

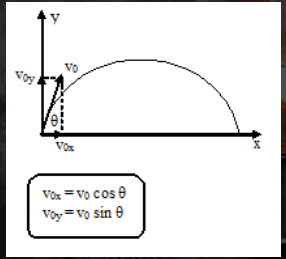
is the motion of an object thrown at an initial velocity v0 in the vertical direction, so that a = -g (against the direction of gravity).
so an object must reach the maximum height (h maks): Vt = 0
In solving the vertical motion problem, more easily solved by assuming the position on the ground is for Y = 0.

Unit vector.

 

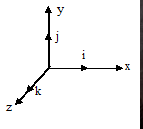
1.Vector that leads to the x-axis unit i.
2.Vector that leads to the y axis j.
3.Vector that leads to z axis k.

Position vector

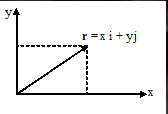
With r is the position vector, x denotes the coordinate point on the x axis and y is the coordinate point on the y axis.

Moving vector

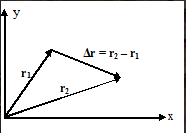
Displacement is a change in the position of a particle in a certain time interval.

With Δr describes the displacement vector and r1 and r2 explain the first and second position vectors.

Vector average speed

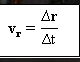
is the quotient between displacement vectors (Δr) at intervals (Δt).

With vr = average velocity vector.

Instantaneous speed vector

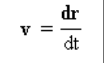
is the first derivative of the position function (r) with respect to time (t).

Vector acceleration average

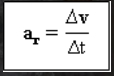
is a change in speed (Δv) in the interval of time (Δt) certain.

Vector acceleration for a moment

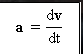
is the first derivative of the speed function (v) with respect to time (t).

Determine the position vector from the velocity vector.

Determine the velocity vector of the acceleration vector.

Circular Motion

• 1. MOVES REGULARLY (GMB)
  GMB is circular motion with angular velocity (w) fixed. The direction of linear velocity v will always offend the trajectory, what that means ,the same as the tangential velocity while the magnitude of v is always fixed (because w remains). makes the radial acceleration ar whose magnitude is constant but the direction changes. ar can also be called always centripetal / centrifugal acceleration | v.

  v = 2pR/T = w Rar = v2/R = w2 Rs = q R

• 2. MOVES ARE CHANGED IN A REGULAR CHANGE (GMBB)
  GMBB is a circular motion with a fixed acceleration angle.
  In this motion there is tangential acceleration aT = linear acceleration, is an acceleration whose direction is toward the circle's trajectory (intersect with the direction of velocity v).
  a = Dw/Dt = aT / R
  aT = dv/dt = a R
  T = perioda (seconds)
  R = circle radius.
  a = angular / angular acceleration (work / DeT2)
  aT = tangential acceleration (m / det2)
  w = angular velocity / angle (row / the)
  q = large angle (radian)
  S = arc length
  Relationship of linear quantities with angular quantities:
  vt = v0 + a t wt
  S = v0 t + 1/2 to t2Þ w0 + a t
  Þ q = w0 + 1/2 a t2
• Angular position (θ) and angular displacement (Δθ).
• 

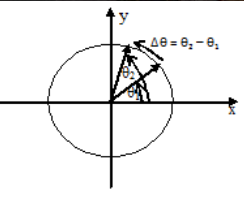
With Δθ can explain angular displacement, θ1 and θ2 explain the position of the first and second angles.

Average angular velocity

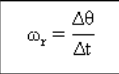
is the result of an angular displacement (Δθ) at intervals (Δt).

Instantaneous angular velocity

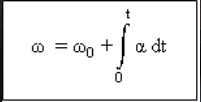
is the first derivative of the angular position function (θ) with respect to time (t).

Vector acceleration average angle

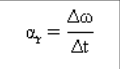
is a change in angular velocity (Δω) in the interval of time (Δt) certain.

Vector acceleration for a momentary angle

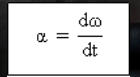
is the first derivative of the angular velocity function (ω) with respect to time (t).

Determine the angular position of the angular velocity.

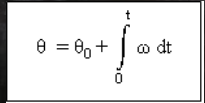
Determine the angular velocity of the angular acceleration.

Parabolic Motion

Time to reach the maximum height.

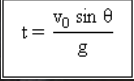
Maximum height

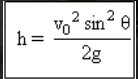
Maximum range / horizontal distance.

 

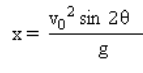
Sample Questions :

1. If a particle moves with the position equation r = 5t2 + 1, average speed between t1 = 2 s and t2 = 3 That's it…
A. 25 m/s
B. 30 m/s
C. 35 m/s
D. 40 m/s
E. 45 m/s

• Information:
  a. First calculate r1 → t1 = 2 s
  r1 = 5t2 + 1 = 5 (2)2 + 1 = 5 . 4 + 1
  r1 = 21 m
  b. Count r2 → t2 = 3 s
  r1 = 5t2 + 1 = 5 (3)2 + 1 = 5 . 9 + 1
  r1 = 46 m
  c. Calculating displacement Δr.
  Δr= r2-r1 =46 -21 = 25 m.
  d. Calculate the average speed of vr.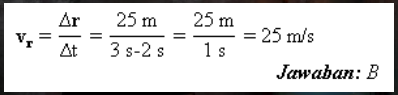
• 
• 2. The position of a point object moving in a flat field is expressed by the equation: r = (5 t2 – 2 t) i + 6 t j with the terms r in meters and t in seconds. The value of the acceleration of the object at t = 2 second is…
  A. 6 m/s2
  B. 10 m/s2
  C. 18 m/s2
  D. 24 m/s2
  E. 28 m/s2
• 

3. The angular velocity of an object is known as follows:
ω = (3t2 + 6t – 2) rad/s, t in second.
At t = 0,5 second, the value of the angular acceleration of the object is…
A. 15 rad / s2
B. 12 rad / s2
C. 9 rad / s2
D. 6 rad / s2
E. 3 rad / s2

4. Objects that move straight have a speed equation:
v = (3 – 6t) i + (4 + 8t) j
The movement of the object during the interval of the second second to the third second is…
A. 10 m
B. 14 m
C. 25 m
D. 42 m
E. 60 m

5. A bullet fired at initial speed 100 m / s and an elevation angle of 30o. If gravity is in that place 10 m/s2, then the time needed for the bullet to reach its highest point is…
A. 2 second
B. 5 second
C. 6 second
D. 10 second
E. 15 second

 

So that's the discussion about

The post Kinematics Material with Vector Analysis and Examples of Problems appeared first on this page.