الفصل الكينماتيكا وتحليل المتجهات

معادلات الحركة هو علم الحركة الذي يناقش حركة الجسم دون النظر إلى القوى المؤثرة على الجسم (يتم تجاهل كتلة الكائن). لذا فإن المسافة التي يقطعها الجسم أثناء حركته لا يمكن تحديدها إلا من خلال السرعة v و/أو التسارع a.

حركة مستقيمة موحدة (GLB)

حركة مستقيمة موحدة (GLB) هي حركة مستقيمة في اتجاه أفقي بسرعة ثابتة v (التسارع أ = 0), بحيث لا تتحدد المسافة التي يقطعها S إلا بسرعة ثابتة في زمن معين.
للحصول على صيغة GLB فإنها تعتمد على قواعد قانون نيوتن الأول ( س ف = 0 ).

الصورة = X = الخامس . ر ;
أ = دف/دت = دف/دت = 0
v = DS/Dt = ds/dt = tetap

علامة د (اختلاف) يذكر متوسط ​​القيمة.
وقع د (التفاضلي) يمثل القيمة اللحظية.

GLBB

تتغير الحركة المستقيمة بشكل موحد (GLBB) هي حركة مستقيمة في اتجاه أفقي بسرعة v والتي يمكن أن تتغير في أي وقت بسبب التسارع المستمر. ومعنى آخر هو أن الجسم الذي يمارس قوة حركية من حالته الأولية من السكون أو يبدأ بسرعة ابتدائية سوف يتعرض لتغير في سرعته بسبب التسارع. (أ= +) أو التباطؤ (أ= -).
عادةً ما يعتمد GLBB على قانون نيوتن الثاني ( س ف = م . أ ).

فت = v0 + في
vt2 = v02 + 2 مثل
S = v0 ر + 1/2 في 2

vt = السرعة اللحظية للكائن
v0 = السرعة الأولية للكائن
S = المسافة التي يقطعها الجسم
F(ر) = دالة الزمن t

ت= س/دت = و (ر)أ = دف/دت = ثابت

متطلبات : إذا تحرك جسمان والتقى كل منهما بالآخر، فإن المسافة التي سيقطعانها هي نفسها.

حركة السقوط الحر

ص = ح = 1/2 GT2

ر = ا(2 ح / ز)

yt = gt = Ö(2 ز ح)
هي حركة جسم يسقط في اتجاه عمودي من ارتفاع معين h بدون سرعة ابتدائية (v0 = 0), مما يجعل حركة الأجسام فقط نتيجة لجاذبية الأرض ز.
g = تسارع الجاذبية الأرضية.
y = h = المسارات التي تتخذها الأجسام في الاتجاه الرأسي,(تقاس من الموضع الأولي للكائن).
t = الزمن الذي يحتاجه الجسم ليقطع مساره.

الحركة الصعودية العمودية

هي حركة الجسم المقذوف بسرعة ابتدائية v0 في الاتجاه الرأسي, بحيث يكون = -g (ضد اتجاه الجاذبية).
لذلك يجب أن يصل الجسم إلى أقصى ارتفاع له (ح ماكس): فاتو = 0
في حل مشكلة الحركة الرأسية للأعلى, من الأسهل حلها بافتراض أن الموضع على الأرض هو Y = 0.

حتى النصر.

 

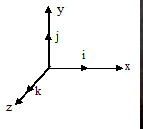
1.المتجه الذي يشير إلى المحور x له وحدة i.
2.المتجه الذي يشير إلى المحور y له وحدات j.
3.المتجه الذي يشير إلى المحور z له وحدات k.

ناقل الموقف

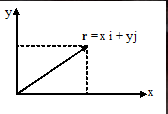
حيث r هو متجه الموضع, تمثل x نقطة الإحداثيات على المحور x وy هي نقطة الإحداثيات على المحور y.

ناقل النزوح

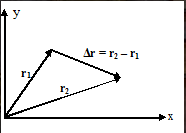
الإزاحة هي التغير في موضع الجسيم خلال فترة زمنية معينة.

مع Δيصف r متجه الإزاحة ويصف r1 وr2 متجهي الموضع الأول والثاني.

ناقل السرعة المتوسطة

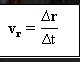
هو حاصل القسمة بين متجهات الإزاحة (Δص) مع مرور الوقت (Δر).

مع vr = متوسط ​​ناقل السرعة.

ناقل السرعة اللحظية

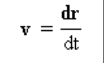
هو المشتق الأول من وظيفة الموقف (ص) ضد الزمن (ر).

متوسط ​​ناقل التسارع

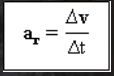
هو تغيير في السرعة (Δالخامس) في مرور الوقت (Δر) تأكيد.

ناقل التسارع اللحظي

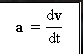
هو المشتق الأول لوظيفة السرعة (الخامس) ضد الزمن (ر).

تحديد متجه الموقع من متجه السرعة.

تحديد متجه السرعة من متجه التسارع.

الحركة الدائرية

• 1. حركة دائرية منتظمة (نشاطي التجاري العالمي)
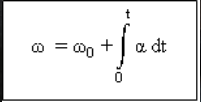
  GMB هي حركة دائرية ذات سرعة زاوية (ث) ثابت: سيكون اتجاه السرعة الخطية v دائمًا مماسًا للمسار, المعنى ,هو نفس اتجاه السرعة العرضية بينما مقدار السرعة v ثابت دائمًا (لأن w ثابت). يؤدي هذا إلى تسارع شعاعي يكون حجمه ثابتًا ولكن اتجاهه يتغير. يمكن أيضًا تسمية ar بالتسارع الثابت للجذب المركزي/الطرد المركزي | الخامس.

  v = 2pR/T = w Rar = v2/R = w2 Rs = q R

• 2. تتغير الحركة الدائرية بانتظام (جي إم بي بي)
  GMBB هي حركة دائرية ذات تسارع زاوي ثابت أ.
  في هذه الحركة يوجد تسارع عرضي aT = تسارع خطي, هو التسارع الذي يكون اتجاهه في مسار دائري (متجمع في اتجاه السرعة v).
  أ = Dw/Dt = AT / ر
  أت = دف/دت = أ ر
  T = الفترة (ثانية)
  R = نصف قطر الدائرة.
  أ = التسارع الزاوي (الخط/it2)
  aT = التسارع العرضي (م/الطفل2)
  ث = السرعة الزاوية/السرعة الزاوية (خط / ذلك)
  س = حجم الزاوية (راديان)
  S = طول القوس
  العلاقة بين الكميات الخطية والكميات الزاوية:
  فت = v0 + بالوزن
  S = v0 ر + 1/2 t2Þ w0 + في
  Þ س = ث0 + 1/2 في 2
• موقف الزاوية (θ) والإزاحة الزاوية (Δθ).
• 

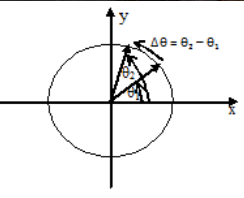
مع Δθ يمكن أن يفسر الإزاحة الزاوية, θ1 و θ2 اشرح موضع الزاويتين الأولى والثانية.

متوسط ​​السرعة الزاوية

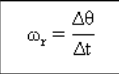
هو الحاصل بين الإزاحات الزاوية (Δθ) مع مرور الوقت (Δر).

السرعة الزاوية لحظية

هو المشتق الأول لوظيفة الموضع الزاوي (θ) ضد الزمن (ر).

متوسط ​​متجه التسارع الزاوي

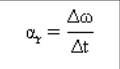
هو التغير في السرعة الزاوية (Δω) في مرور الوقت (Δر) تأكيد.

ناقل التسارع الزاوي اللحظي

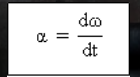
هو المشتق الأول لوظيفة السرعة الزاوية (ω) ضد الزمن (ر).

تحديد الموقع الزاوي من السرعة الزاوية.

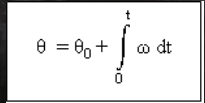
تحديد السرعة الزاوية من التسارع الزاوي.

حركة مكافئة

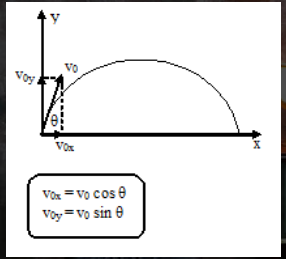
الوقت للوصول إلى أقصى ارتفاع.

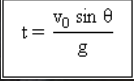
أقصى ارتفاع

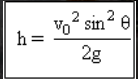
أقصى مدى/مسافة أفقية.

 

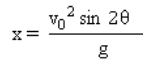
مثال المشاكل :

1. إذا تحرك جسيم بمعادلة الموضع r = 5t2 + 1, متوسط ​​السرعة بين t1 = 2 الصورة وt2 = 3 هو…
أ. 25 آنسة
ب. 30 آنسة
ج. 35 آنسة
د. 40 آنسة
ه. 45 آنسة

• معلومة:
  أ. أولا احسب r1 → t1 = 2 س
  ص1 = 5ت2 + 1 = 5 (2)2 + 1 = 5 . 4 + 1
  ص1 = 21 م
  ب. حساب r2 → t2 = 3 س
  ص1 = 5ت2 + 1 = 5 (3)2 + 1 = 5 . 9 + 1
  ص1 = 46 م
  ج. حساب النزوح Δص.
  Δص = ص2-ص1 =46 -21 = 25 م.
  د. حساب متوسط ​​سرعة vr.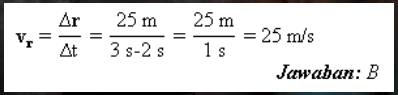
• 
• 2. يتم التعبير عن موضع جسم نقطي يتحرك في المستوى بالمعادلة: ص = (5 t2 – 2 ر) أنا + 6 t j حيث r بالمتر و t بالثواني. قيمة عجلة الجسم عند الزمن t = 2 الثاني هو…
  أ. 6 م/ث2
  ب. 10 م/ث2
  ج. 18 م/ث2
  د. 24 م/ث2
  ه. 28 م/ث2
• 

3. تُعرف السرعة الزاوية لجسم ما على النحو التالي:
ω = (3t2 + 6ر – 2) راد / ث, ر في ثوان.
عند ر = 0,5 ثانية, قيمة التسارع الزاوي للجسم هي…
أ. 15 rad/s2
ب. 12 rad/s2
ج. 9 rad/s2
د. 6 rad/s2
ه. 3 rad/s2

4. الأجسام التي تتحرك في خط مستقيم لها نفس السرعة:
الخامس = (3 – 6ر) أنا + (4 + 8ر) ي
إزاحة الجسم خلال الفترة الزمنية من الثانية الثانية إلى الثانية الثالثة هي…
أ. 10 م
ب. 14 م
ج. 25 م
د. 42 م
ه. 60 م

5. يتم إطلاق الرصاصة بسرعة ابتدائية 100 م/ث وزاوية الارتفاع 30 درجة. إذا كانت الجاذبية في ذلك المكان 10 م/ث2, فالزمن اللازم للرصاصة للوصول إلى أعلى نقطة هو…
أ. 2 ثانية
ب. 5 ثانية
ج. 6 ثانية
د. 10 ثانية
ه. 15 ثانية

 

هذا هو النقاش بخصوص

ظهرت المادة الحركية مع التحليل المتجه وأسئلة الأمثلة أولاً على هذه الصفحة.